피보나치 수열(Fibonacci numbers)

피보나치 수열은 다양한 알고리즘에서 사용되며 재귀의 좋은 예시를 제공합니다. 해당 포스팅을 통해 피보나치의 수열을 이해하고 활용 방법에 대해 정리하려고 합니다.

 

피보나치 수열(Fibonacci numbers)이란?

---

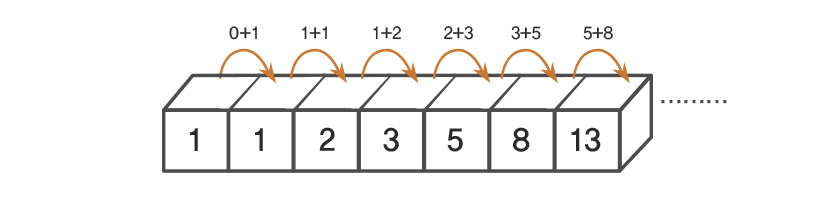
이전 두 항의 합이 다음 항이 되는 수열을 의미합니다. 첫 번째와 두 번째 항이 1이고, 세 번째 항부터는 이전 두 항의 합으로 이루어지는 규칙을 따릅니다.

피보나치 수열의 첫 번째 항은 f(0), 두 번째 항을 f(1)으로 정의합니다.

• f(0) = 1
• f(1) = 1

이때 n번 째 항은 (n - 1)번째 항 + (n - 2)번째 항입니다.

• f(n) = f(n-1) + f(n-2)

피보나치 수열의 첫 번째 항부터 순서대로 예시를 본다면 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ... 로 구성됩니다.

 

즉 정리하면 피보나치 수열의 연산식은 다음과 같습니다.

f(0) = 0, f(1) = 1 일 때
f(n) = f(n - 1) + f(n - 2) 단, (n ≥ 2) 일 경우

💡 피보나치 수열 예시
예시로 n이 3이라면 f(n - 1) + f(n - 2)로 정의됩니다.
 ・ f(3) = f(3 - 1) + f(3 - 2)
 ・ f(3) = f(2) + f(1)
 ・ f(3) = 1 + 1
 ・ f(3) = 2
만약 n이 4일 경우 f(3) + f(2) 임으로 2 + 1 = 3이 됩니다.

 

---

 

피보나치 수열 구현 방식

---

피보나치 수열을 구현하는 방식은 주로 3가지로 나뉩니다. 반복문, 재귀 함수, 동적 계획법입니다. 각각의 방식은 피보나치 수열을 다른 방식으로 접근하며, 각각의 장단점이 있습니다.

구현 방식	장점	단점
반복문	메모리 사용량을 최소화하며, 일정 크기 내에서 연산이 효율적이다.	크기가 큰 경우 연산 속도가 많이 소요된다.
재귀 함수	코드가 간결하여 이해하기 쉽다.	재귀 호출로 인한 중복 연산으로 효율성이 떨어지며, 스택 오버플로우가 발생할 가능성이 있다.
동적 계획법	중복되는 연산을 피하여 효율성이 높다.	다른 방식에 비해 메모리 사용량이 높다.

 

1. 반복문(Loop)

---

반복문을 활용하여 피보나치 수열을 계산합니다. 이전 항들을 반복적으로 계산하여 현재 항을 구하는 방식으로 과정은 다음과 같습니다.

1. 첫 번째 항과 두 번째 항은 모두 1이므로, n ≤ 2인 경우 1을 반환합니다.
2. 세 번째 항부터 반복문을 순회하며 n번째 항까지 계산합니다.
3. 현재 항(n)은 이전 두 항(n -1, n-2)의 합으로 계산되며, 계산된 값은 이정 항들의 값을 경신하여 다음 항을 계산할 수 있도록 합니다.

public static int fibonacci(int n) {
    if (n <= 2) {
        return 1;
    }

    int answer = 0;
    int prev1 = 1;
    int prev2 = 1;

    for (int i = 2; i < n; i++) {
        answer = prev1 + prev2;
        prev1 = prev2;
        prev2 = answer;
    }

    return answer;
}

 

2. 재귀 함수(Recursive Function)

---

재귀적 정의에 따라 함수를 호출하여 계산합니다. 즉 함수 자신을 재호출하는 방식입니다.

1. 첫 번째 항과 두 번째 항은 모두 1이므로, n ≤ 2 인 경우 1을 반환합니다.
2. 그 외의 경우 현재 항을 이전 두항의 합으로 계산하기 위해 재귀 호출합니다.

public static int fibonacci(int n) {
    if (n <= 2) {
        return 1;
    }

    return fibonacci(n - 1) + fibonacci(n - 2);
}

💡 재귀 함수(Recursive Function)란?
함수 자기 자신을 호출하는 것을 허용하는 함수입니다. 이는 함수가 어떤 작업을 수행하기 위해 자기 자신을 다시 호출할 수 있으며, 보통 재귀 호출을 통해 작은 문제를 해결하고, 이를 조합하여 더 큰 문제를 해결하는 데 사용됩니다.

재귀 함수는 보통 기저 조건(base case)과 재귀 호출(recursive call)로 이루어져 있습니다. 기조 조건은 함수가 자기 자신을 호출하지 않고 바로 반환하는 경우로, 재귀를 종료시키는 역할을 합니다. 재귀 호출은 함수가 자기 자신을 호출하여 더 작은 입력 값에 대해 작업을 수행하는 것을 의미합니다. 재귀 호출은 입력 값이 점점 작아지며 입력 값이 기저 조건에 부합될 때 종료됩니다.

 

3. 동적 계획법(Dynamic Programming)

---

동적 계획법은 중복되는 계산을 피하기 위해 이전에 계산한 값을 저장하여 재활용하는 방식입니다.

1. 재활용이 될 값을 저장하기 위한 배열을 생성합니다.
2. 첫 번째와 두 번째 항을 1로 초기화하여  기저 조건을 설정합니다.
3. 반복문을 사용하여 세 번째 항부터 n번째 항까지 계산하여 저장합니다.

public static int fibonacci(int n) {
    int[] dp = new int[n + 1];
    dp[1] = 1;
    dp[2] = 1;

    for (int i = 3; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }

    return dp[n];
}

💡 동적 계획법(Dynamic Programming)이란?
복잡한 문제를 간단한 여러 하위 문제로 나눠 푸는 방식으로 하위 문제의 해결 방법을 저장하고 재활용하여 전체 문제를 효율적으로 해결합니다. 동적 계획법은 중복 계산 대신 저장된 값을 재활용하기 때문에 효율성이 높습니다.

 

---

자연과 디자인에서 찾을 수 있는 ‘피보나치 수열’에 숨은 황금비!

알고리즘 - Dynamic Programming(동적 계획법)